每一種題目可能有數種的解法，那我們應該怎麼評估每種解法的優劣呢?以前的我應該會回答，當然是越簡短的寫法越好呀! 不過，寫過leetcode之後，會發現有時候很簡短的解法，執行效率反而看不見別人的車尾燈(吊車尾)，那麼leetcode是怎麼評斷解法的好壞呢? 答案是透過時間複雜度和空間複雜度來評估。

• 時間複雜度(Time Complexity):執行函式需要花費的時間
• 空間複雜度(Space Complexity):執行函式會占用的記憶體空間

關於時間複雜度

• 演算法運算次數的增長效率
• 演算法的執行時間不是以秒計算的， 是以運算次數計算的
• 演算法的執行時間 ，不一定會隨著元素數量的增加而等比增加

這邊要特別注意，執行的時間並非以秒為單位，因為家用電腦與超級電腦的運算速度根本天差地遠，比較秒數的話其實沒有多大的意義，因此是用次數來作計算，而我們習慣用O來表示演算法的執行效率，作為評估演算法執行效率好不好的指標，當函式輸入的Input 長度變長的時候，就可以了解演算法的效率趨勢，效能差的演算法的曲線就會陡峭上升像是O(n²)而好的演算法的曲線會趨於平緩O(log n)。

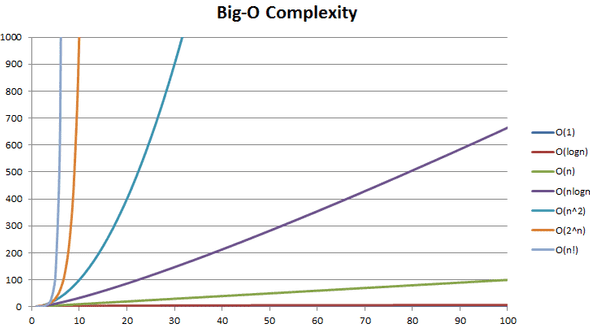
*圖片來源:*https://smootok.com/big-o-notation/

O(1) - 常數

不管輸入的n為多少，都只要執行一次

//無論arr的length有多長，都只要執行一次即可
//ex : 找出index=2的值為何?
const arr = ['andy', 'peggy', 'debby'] 
console.log(arr[2])

O(log n) - 對數(n 是 2 的幾次方)

輸入8的話，log 8 = 3，也就是8 = 2³ (8是n的3次方)，所以經過3個步驟就可以找到我們要的答案，簡單來說就是不斷的剖半，像是二分搜尋法

O(n) - 線性

跑一次迴圈，所以如果輸入的n越長，執行的次數也會等比增加

//找出這個陣列有沒有debby這個人,不用indexOf和includes話，就是土法煉鋼，從頭找到尾，一個一個慢慢找
const arr = ['andy', 'peggy', 'debby']
for(let i=0;i<arr.length;i++){
    if(arr[i]==='debby') return true;
}

O(nlog n) - 線性對數

ex:快速排序法，在之後的文章會有更詳細的解說

O(n²) - 平方，n的平方

ex:用雙迴圈印出一個九九乘法表

//n*n=n²
for(let i=1; i<=9; i++){
   for(let j=i; j<=9; j++){
      console.log(`${i}*${j} = ${i*j}`)
   }
}

O(n!) - 階乘

ex:n階乘，ex: n x n-1 x … x 3 x 2 x 1

最理想的時間複雜度就是O(log n)或是O(1)

關於空間複雜度

執行程式佔用的記憶體空間 ，占用越多越吃資源，一樣也是用Big O來表示，而時間複雜度和空間複雜度兩者是可以互相trade off的。

甚麼是trade off?

有時候可以用空間來換取時間 ，或是用時間換取空間，依照當時的使用情境來做取捨。

O(1)
不管輸入的n為多少，都只會建立一個變數total，因此空間複雜度為O(n)

const add = (n) =>{
    let total = 0
    for(let i=0;i<n;i++){
       total += i
    }
    return total
}

O(n)
arr的長度會根據使用者輸入的n來增長，因此空間複雜度為O(n)

const createArray = (n) =>{
    const arr = []
    for(let i=0;i<n;i++){
        arr.push(i);
    }
    return arr
}